Geometry 1
Here I’ll share some Codeforces problems I solved by visualizing what happens on a 2D plane. The tricks I discuss here rely on checking parity, the pigeonhole principle and Dilworth’s Lemma.
Two Hundred Twenty One
In this problem, we are given a sequence of $N$ numbers. Each number can be either $+1$ or $-1$.
i : 0 1 2 3 4 5 6 7 8 9 10 11 12
a_i: +1 -1 +1 +1 +1 -1 +1 +1 -1 -1 +1 -1 +1
For a range of the array $i \in [l, r]$, there is an alternating sum:
\[S_{lr} = \sum_{i = l}^r (-1)^{i - l} a_i\]l r S_lr
-----------
0 0 1
0 3 2
1 3 -1
Given a range $[l, r]$, we have to find the minimum number of elements in range that we should remove so that the alternating sum becomes $0$. We are given a lot of such queries so we would like to compute the answer fast (in $O(1)$).
This is a very weird problem and like many Codeforces problems, it is unlikely that we’ll come across it in the real world. Nevertheless, analysing it is quite fun. Earlier, I had a lot of trouble in initiating the analysis. I was a bit lost about what questions I should ask. Now Ifind it helpful to see what happens when one thing changes. In the present case, let’s see what happens when we remove one element from the sequence.
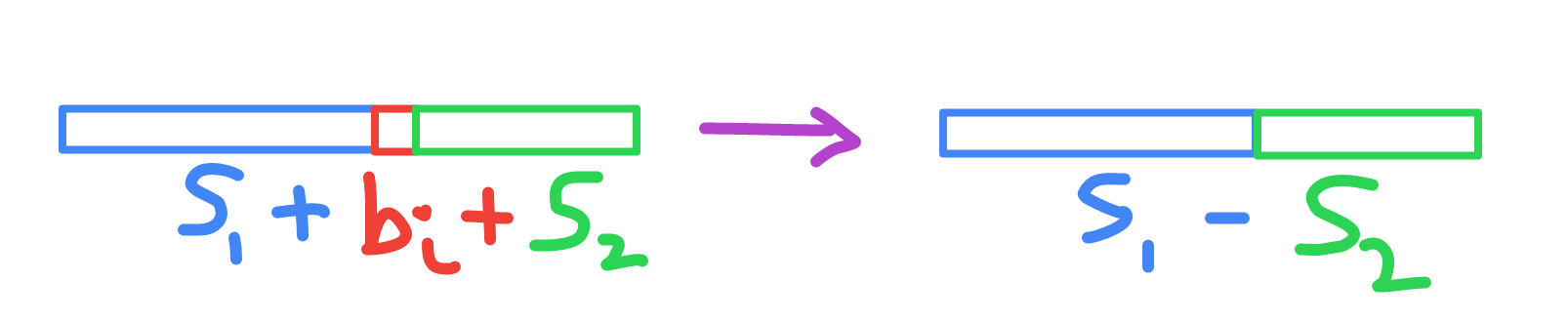
In the image, $b_i$ takes into account the sign that $a_i$ was multiplied with while computing $S_{lr}$. Since $b_i$ is $\pm 1$ after removing it, the parity of the initial sum changes. If $S_{lr}$ is even initially, it becomes odd and vice versa. We can use this fact to lower-bound the number of times we need to remove an element. Since $0$ is even, if $S_{lr}$ is odd, we need remove at least $1$ element. On the other hand, if $S_{lr}$ is even and not $0$, then we need to remove at least $2$ elements.
In this problem, it turns out that we can always achieve these lower-bounds. To see this, let’s visualize the problem on a graph. Fix $l = 0$ and plot $S_{0r}$ for different $r$.
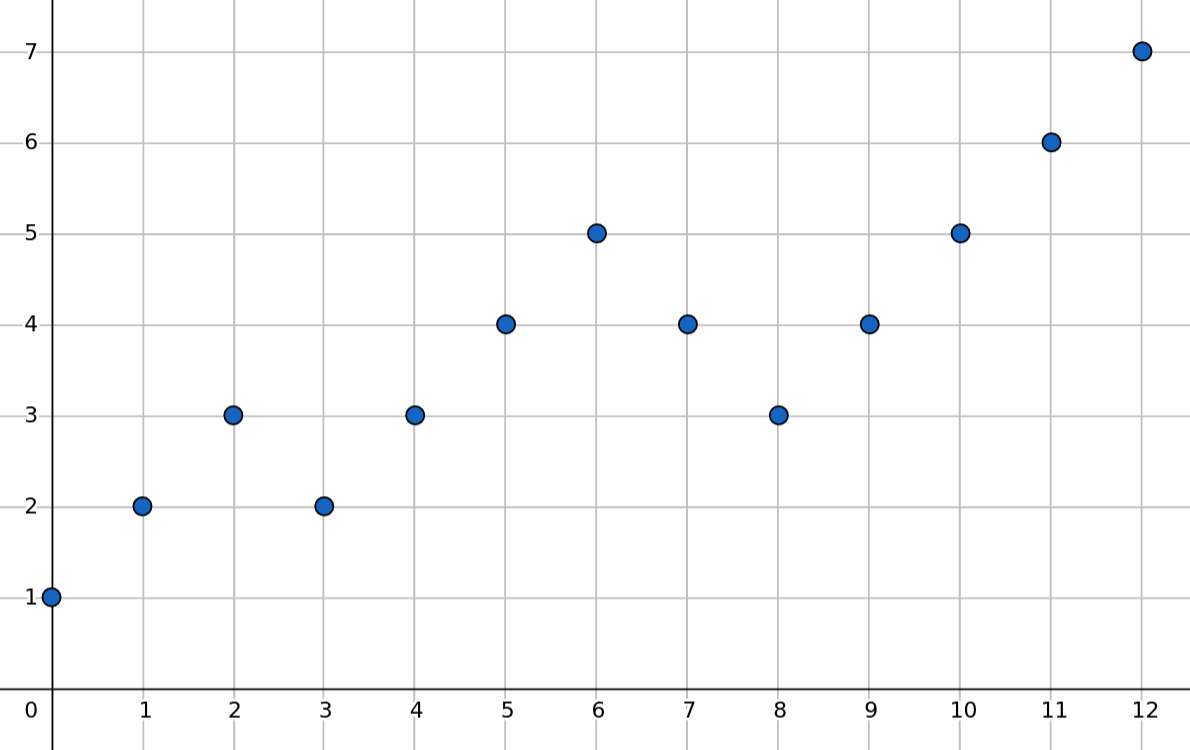
The alternating sum of the entire array is $7$. If there was an index $j$ such that $S_{0j} = 3$, then we could just remove the element at $j + 1$ and obtain an alternating sum of $0$. Such a $j$ always exists. This is because $S_{0r}$ changes by $1$ at each $r$. You can think of it as a discrete version of the Intermediate Value Theorem from Calculus. In our example $j = 4$.
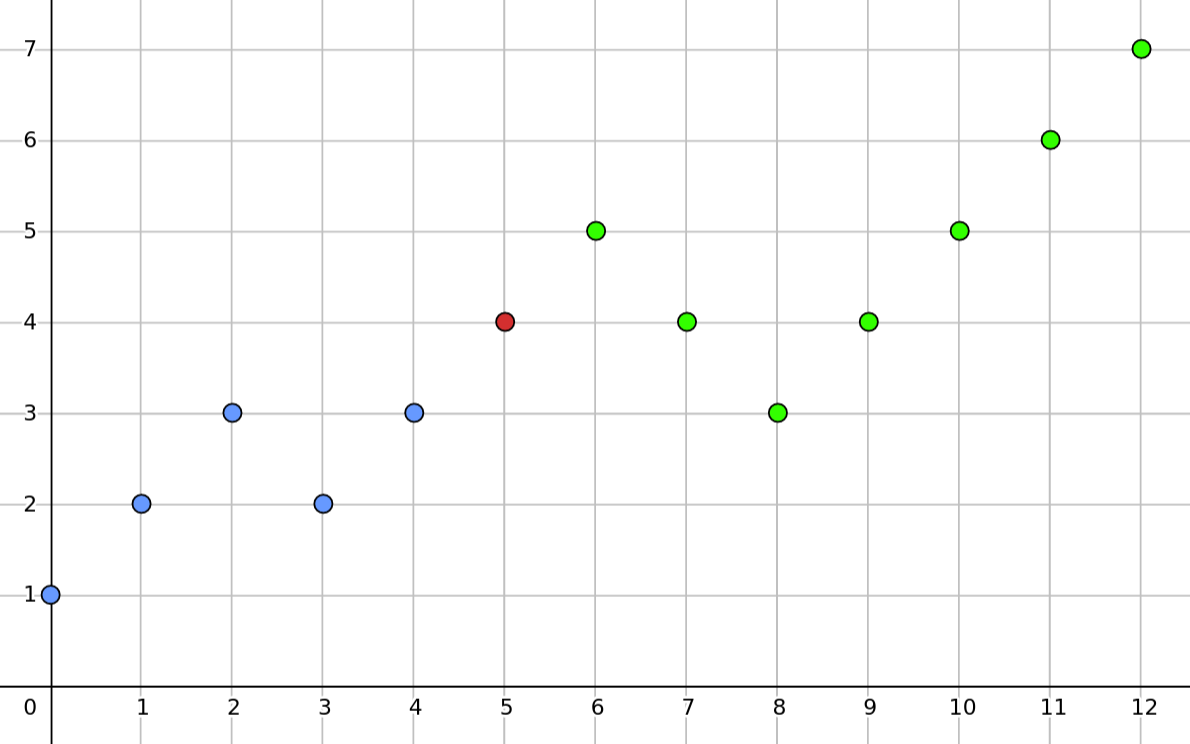
After removing the red point, the green part will mirror about the x-axis, making the alternating sum $0$. Generalizing this observation, if $S_{lr}$ is odd, then we can always make the alternating sum $0$ by removing just $1$ element. We find the index $j$ such that $S_{lj} = \frac{S_{lr} - 1}{2}$ and remove the element at $j + 1$. If $S_{lr}$ is even, we remove any element to make the alternating sum odd. Then, we make the alternating sum $0$ using the trick above.
In order to answer queries, simply compute the alternating sum in the given range. If the alternating sum if odd, the answer is $1$, if even and not $0$, the answer is $2$. The alternating sum can be computed for any range in $O(1)$ using prefix-sums.
Training Session
We are given $[n]$ and two arrays $A_1 \cdots A_n$ and $B_1 \cdots B_n$. All pairs $(A_i, B_i)$ are distinct. We have to find the number of ways we can select three distinct numbers $i, j, k \in [n]$ such that one of the following is true:
- $A_i$, $A_j$, $A_k$ are distinct.
- $B_i$, $B_j$, $B_k$ are distinct.
I wasn’t able to count these directly. Instead, I counted the triplets that don’t satisfy this condition (the bad triplets). The final answer was the difference between all $nC3$ possible triplets and the bad triplets.
Negating the conditions above, we find that bad triplets have to satisfy both of the following:
- Any two of $A_i$, $A_j$ and $A_k$ are the same.
- Any two of $B_i$, $B_j$ and $B_k$ are the same.
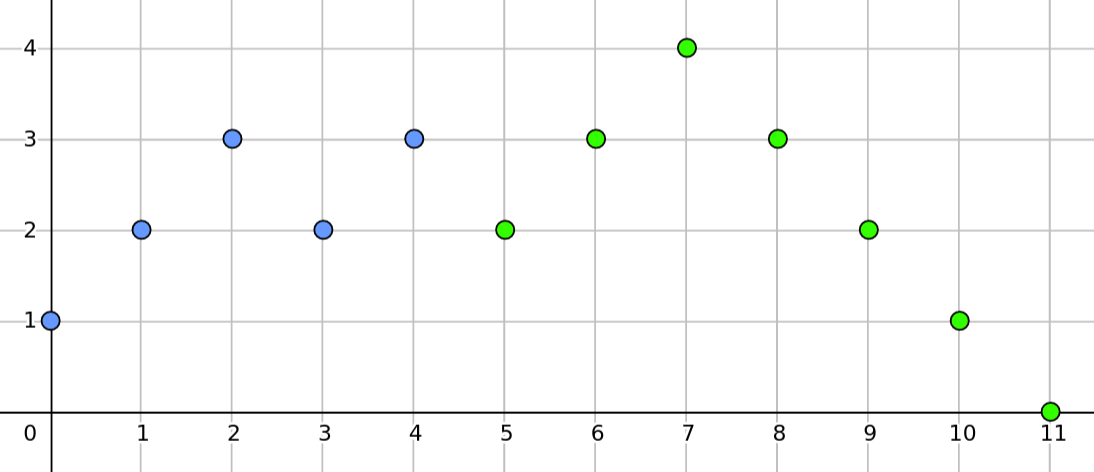
Again, plotting $(A_i, B_i)$ on a graph gave a way to count bad triplets. On a graph, you can immediately see that bad triplets form an L (eg. points $1, 3, 4$ in the image below). This is because of Pigeonhole Principle which says that if there are more pigeons than holes, then some hole has more than two pigeons. It is a stupid principle, much like the pigeons themselves.
Anyway, to see why bad triplets always make an L, let $i_1, i_2$ be the indices for which $a_{i_1} = a_{i_2}$ and $j_1, j_2$ be the indices for which $b_{j_1} = b_{j_2}$. Since these are indices in a triplet (the holes), all of $i_1, i_2, j_1, j_2$ (the pigeons) can’t be distinct. Some $i_{k_1} = j_{k_2}, k_1, k_2 \in \{1, 2 \}$. In the image, the common index is $3$. Let’s refer to this common index as the pivot.
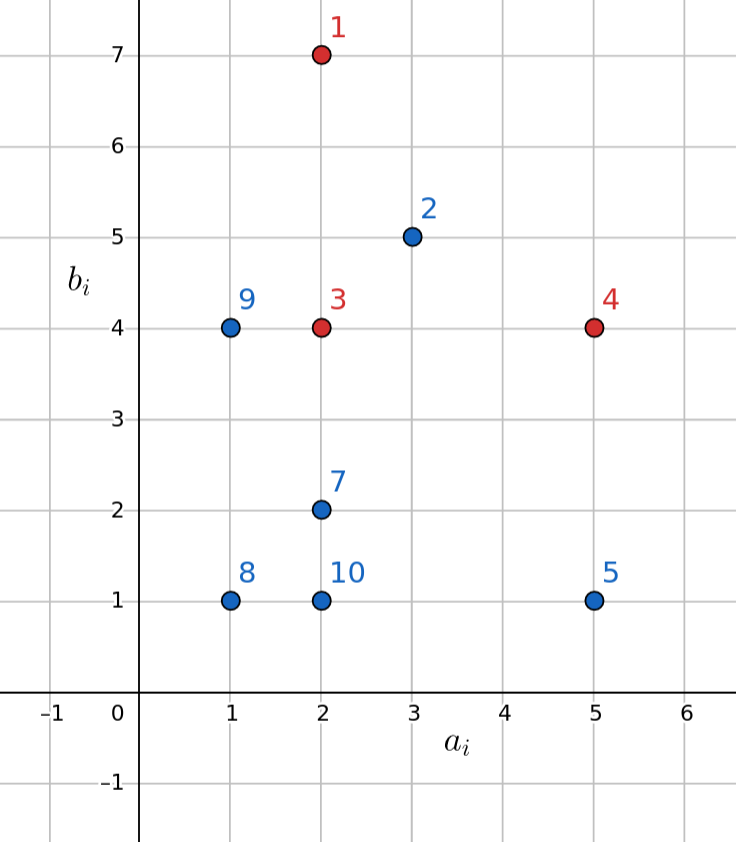
We’ll count the bad triplets by counting bad triplets in which a each index is a pivot. There will be bad triplets with $1$ as the pivot, $2$ as the pivot, $3$ as the pivot and so on. All these subsets will be disjoint and their union will be the set of all bad triplets. We’ll get the sizes of these subsets individually and sum them up.
When an index $i$ is a pivot, one member of the triplet is horizontal to it and the other is vertical to it. If we count indices having the same $B$-value and $A$-value (Bcnts[b] and Acnts[a]), then the number of bad triplets with $i$ as the pivot are (Bcnts[B[i]] - 1) * (Acnts[A[i]] - 1). We subtract one to avoid counting $i$ twice in the triplet. Referring to the image, you can see that the number of bad triplets in which $3$ is the pivot are $2 \times 3 = 6$.
By precomputing Bcnts and Acnts, we can count the bad triplets in $O(n)$ by iterating over all possible pivots and adding their contribution using the formula above. To solve the original problem, we subtract this number from $nC3$, the number of triplets in total.
Manhattan Subarrays
I like this problem because it is an interesting application of the Dilworth’s Lemma. We are given an array $a_1 \cdots a_n$. A triplet of distinct indices $i, j, k$ is considered bad if:
\[\underbrace{|a_i - a_j| + |i - j|}_\textrm{manhattan distance between i, j} = \underbrace{|a_i - a_k| + |i - k|}_\textrm{manhattan distance between i, k} + \underbrace{|a_k - a_j| + |k - j|}_\textrm{manhattan distance between k, j}\]A contiguous subarray $a_l \cdots a_r$ is considered good if we can’t pick any bad triplet from it. We have to count the number of good subarrays.
I found the definition of a bad triplet quite convoluted. I searched for simpler but equivalent definitions of bad triplets. I simplified the problem by asking this question in one dimension. When does the following happen?
\[|a_i - a_j| = |a_i - a_k| + |a_k - a_j|\]This happens if and only if $a_k$ is between $a_i$ and $a_j$. The image below illustrates that when $a_k$ is between $a_i$ and $a_j$ then LHS and the RHS are equal. When it is not, such as for $a_{k’}$, then the segment $|a_i - a_{k’}|$ on its own is longer than $|a_i - a_j|$. In this case:
\[|a_i - a_j| < |a_i - a_{k'}| + |a_{k'} - a_j|\]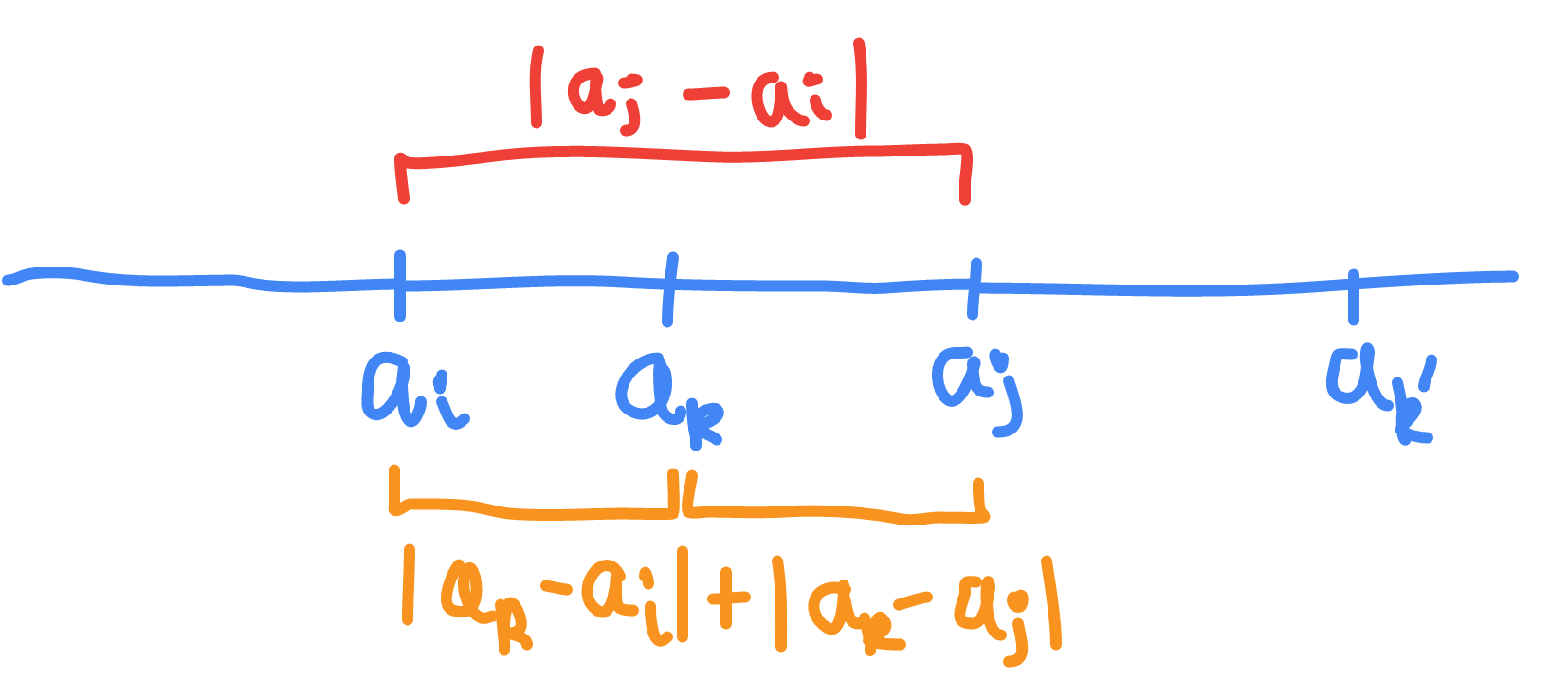
Back in our original two dimensional problem, we can infer that if $a_k$ is between $a_i$ and $a_j$, then $k$ is between $i$ and $j$.
\[\cancel{|a_i - a_j|} + |i - j| = \cancel{|a_i - a_k|} + |i - k| + \cancel{|a_k - a_j|} + |k - j|\] \[\Rightarrow k\text{ is between }i\text{ and } j\]Likewise, if $k$ is between $i$ and $j$ then $a_k$ is between $a_i$ and $a_j$. On the other hand, when $k$ is not between $i$ and $j$, then $a_k$ is not between $a_i$ and $a_j$. In this case, the triplet $i, j, k$ is not bad. Visualizing bad triplets on a graph, observe that they form a monotonic sequence.
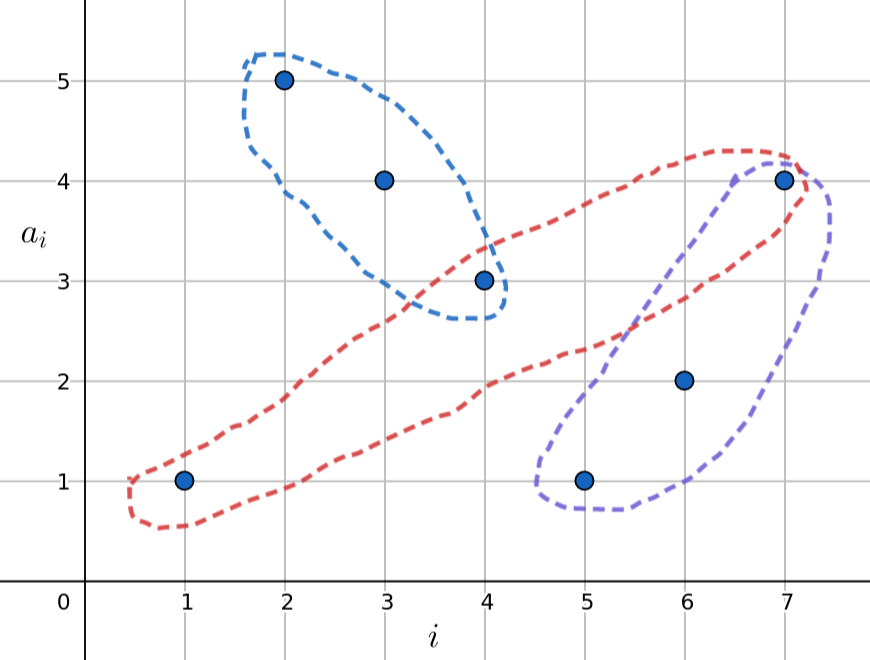
As you can imagine, good subarrays i.e. those that don’t contain bad triplets, can’t be too long. If they are small enough, then we can simply enumerate all of subarrays upto some size and count the good ones. We can obtain a bound on the size of good subarrays using partial orders and Dilworth’s Lemma.
Define a partial order as $(a_i, i) \leq (a_j, j)$ if $i \leq j$ and $a_i \leq a_j$. The image below shows what this partial order looks like. The directed arrow indicates when one point is $\leq$ than the other. If $x \leq y$ and $y \leq z$ than $x \leq z$ and so I haven’t bothered to draw the arrows from $x$ to $z$.
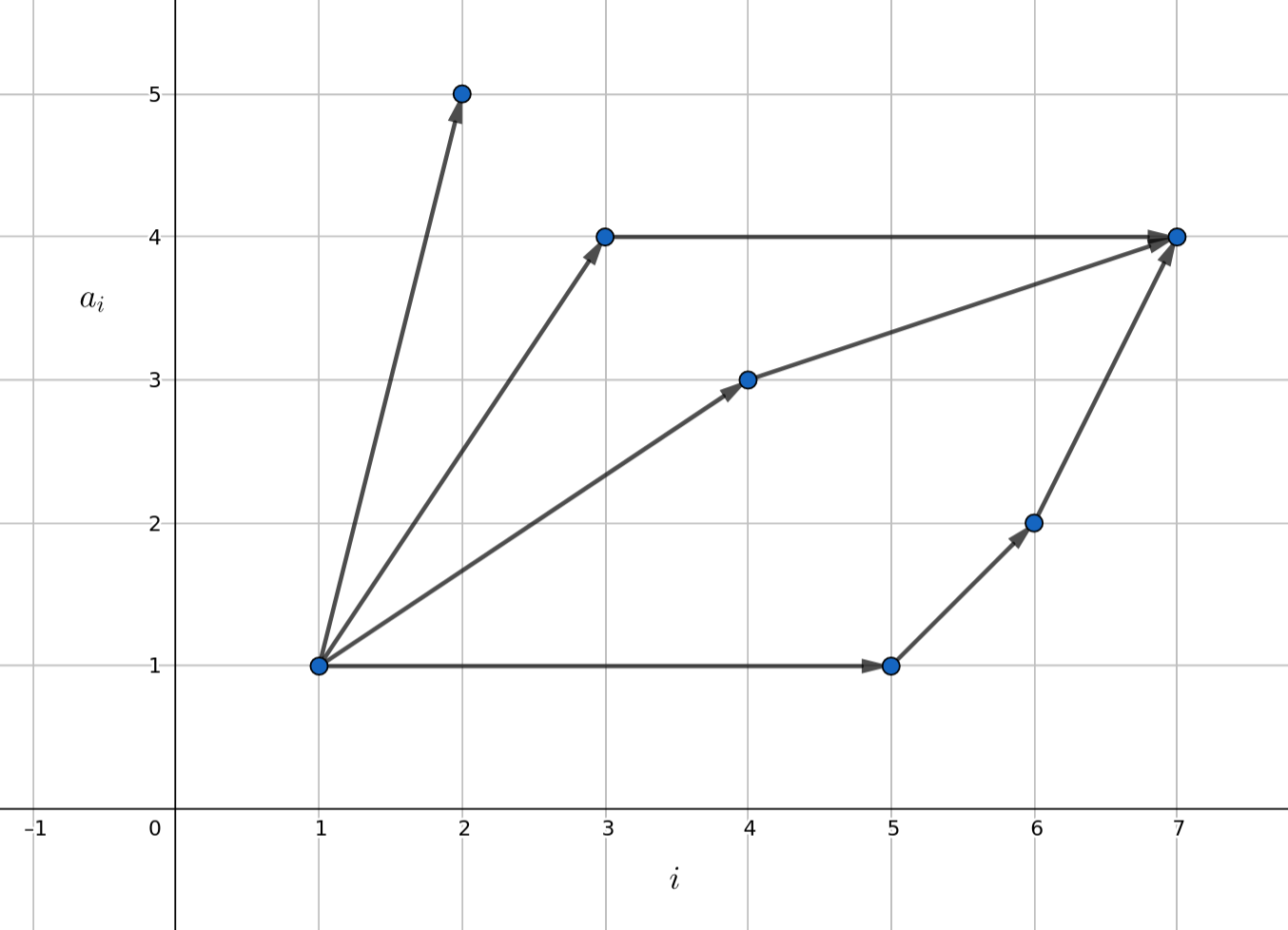
Notice that unrelated points i.e. points where neither is $\leq$ than the other, form a decreasing sequence. By Dilworth’s Lemma, in a subarray of length $N$, either there is an increasing subsequence of length greater than $\sqrt{N}$ or a decreasing subsequence of length greater than equal to $\sqrt{N}$. If a subarray has length greater than $4$, then Dilworth’s Lemma tells us that it is bound to be bad.
Now, we can count good subarrays by enumerating all subarrays of size at most $4$ and checking whether they are good. The time complexity of doing so is $O(n)$.
Conclusion
Visualizing problems helps a lot obviously. Also, the steps in the solutions presented above didn’t occur to me in the linear order in which they are presented. There are a lot of tiny failure tracks that I have trimmed while writing this. This just means that when you are solving problems, you are going to be led down the proverbial garden path. And that is ok!
I recommend reading the post that explains Dilworth’s Lemma. In fact, that MIT OCW course is quite good on the whole.